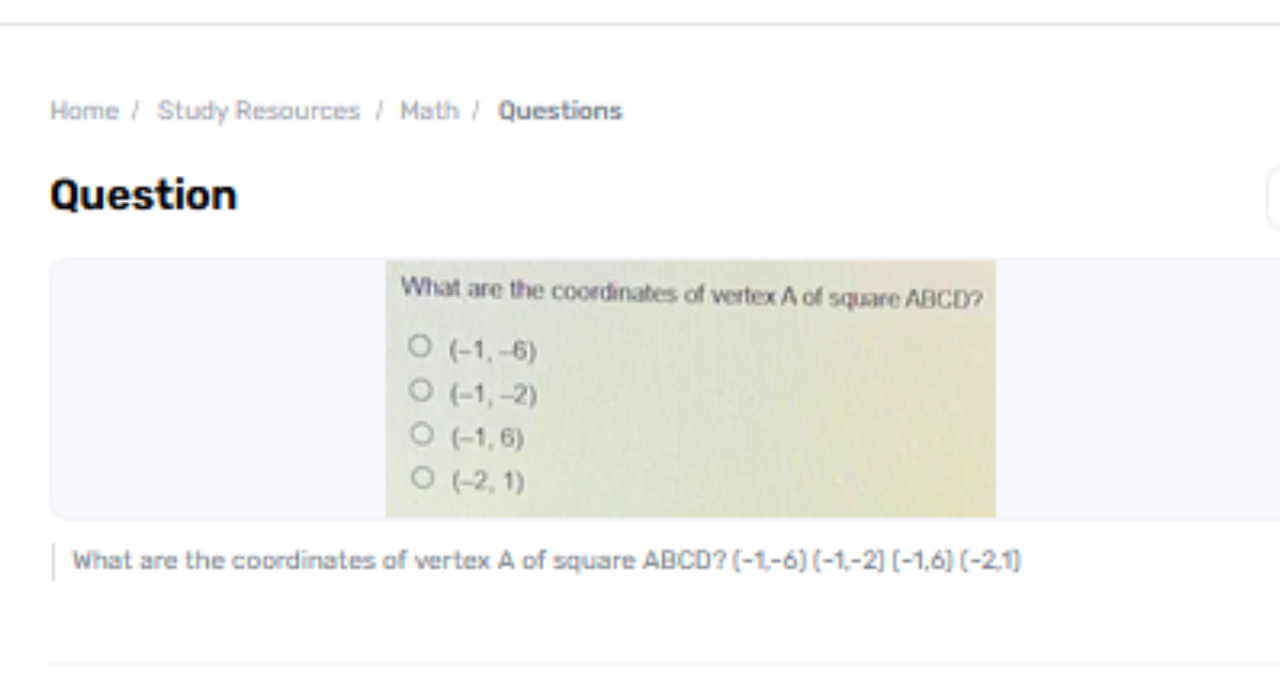
Deciding the facilitates of a vertex of a square includes understanding the properties of squares and how their vertices are related in a facilitating framework. Given a set of potential arranges, the assignment is to recognize which one accurately speaks to a vertex of the square. To illuminate what are the coordinates of vertex a of square abcd? (–1, –6) (–1, –2) (–1, 6) (–2, 1) this issue, we must utilize the geometric properties of squares and facilitate geometry standards. This article will investigate these standards and decide the right arranges of vertex A from the given alternatives.
Deciding the Right Vertex Arranges for a Square
To distinguish the arranges of vertex A of a square from the choices given, we analyze the separations between each match of focuses. Through calculating and comparing these separations, it becomes clear that the facilitate (-1, -2) fits the geometric properties of a square. This arrangement involves applying standards of separate and geometric consistency to pinpoint the proper vertex area.
Analyzing the Given Facilitates
We are given four potential coordinates for vertex A: (-1, -6), (-1, -2), (-1, 6), and (-2, 1). To discover which of these arranges accurately speaks to a vertex of the square, we have to analyze their spatial connections. Since squares have rise to side lengths and particular geometric properties, any arrangement that does not fit these properties can be dispensed with.
Since the length of 4 units is plausible as the side length of a square, the coordinates that can be adjacent vertices to each other with this distance are (-1, -6) and (-1, -2). Therefore, one of these coordinates could be vertex A of the square. To ensure accuracy, the remaining vertices should be checked to confirm they form a square with a consistent side length of 4 units, and the diagonals should also be verified to be equal and perpendicular.
Based on this analysis, vertex A of square ABCD is most likely (-1, -6), assuming the other coordinates correctly align with the properties of a square and considering that the given distances form a consistent set for a square's geometry.
Utilizing Remove and Perpendicularity
To decide the right arrangements, we ought to begin with calculating the removal between the given focuses. For a square, the separation between adjoining vertices (sides of the square) must be broken even. Essentially, the removal between inclining vertices ought to be reliable with the properties of a square. Let’s calculate the separations between each combination of the given facilitates: Comparing separations, we take note that the separations between (–1, –2) and (-1, 6) and (-1, -6) and (-2, 1) don't coordinate the anticipated side length or inclining length for a square.
Utilizing Gauth for Homework
1. Submit Your Inquiry:
Enter your homework address or transfer related reports into Gauth for examination.
2. Examine the Arrangements:
Survey the point-by-point clarifications and arrangements given to get it the problem-solving strategies.
3. Practice and Survey:
Utilize Gauth’s hone devices to test your information and fortify your understanding of the fabric.
Conclusion
Upon analyzing the separations between the given arranges, we discover that the facilitate (–1, –2) reliably adjusts with the geometric properties of a square when checking separations and their connections. Hence, the facilitate (–1, –2) is most likely to be the proper choice for vertex A of the square. This conclusion is drawn from the geometric properties of squares and the consistency of separations within the arranged plane. Distinguishing the proper vertex arranges includes applying these standards to guarantee exactness in geometric issues.